Ok, ich hab' zwar noch keine Lösung, aber ich schreib einfach mal, was ich so denke.

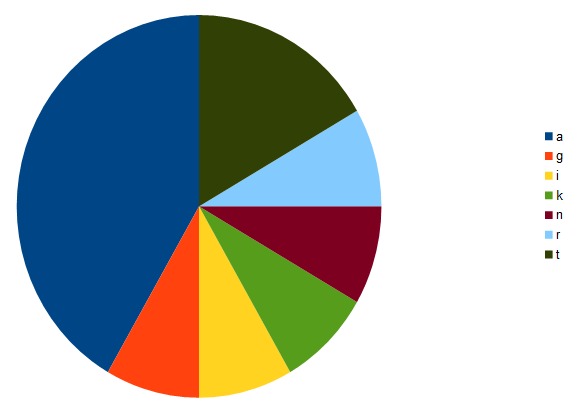
Wir haben einen Kreis, der in Drittel unterteilt ist, darunter:
- a - 5/3
- t - 2/3
- g, i, k, n, r - je 1/3
Auffällig ist, dass ausgerechnet der erste und der letzte Buchstabe nicht 1/3 entspricht.
Außerdem sind die Buchstaben jeweils mit einem gewissen Abstand zum vorherigen Buchstaben angeordnet.
a {1} [5/3]
(+6) -> g {7} [1/3]
(+2) -> i {9} [1/3]
(+2) -> k {11} [1/3]
(+3) -> n {14} [1/3]
(+4) -> r {18} [1/3]
(+2) -> t {20} [2/3]
Ich vermute, dass man den Wert der Zahl, vielleicht auch die Nummer im Alphabet und den Abstand verrechnen muss, um auf Buchstaben zu kommen.
Ob die Differenz zum Vorgänger oder zum Nachfolger gehören soll, ist nicht ganz klar, vermutlich aber eher zum Nachfolger.
Allerdings sind die Abstände teilweise so regelmäßig, dass das die Theorie unwahrscheinlich erscheinen lässt. Müsste man nur die Buchstaben neu berechnen, dürften die Ausgangsbuchstaben keine so glatte Reihe ergeben, zumal die meisten Buchstaben auch den Wert 1/3 im Diagramm haben. Es ist also auch unwahrscheinlich, dass man die Buchstaben dann neu zusammenwürfeln muss.
Mal zwei Ansätze:
5 - 6+1 - 2+1 - 2+1 - 3+1 - 4+1 - 2+2 -> e - g - c - c - d - e - d
1+5 - 7+6*1 - 9+2*1 - 11+2*1 - 14+3*1 - 18+4*1 - 20+2*2 -> f - m - k - m - q - v - x
Scheint mir sehr falsch zu sein.

Außerdem wäre es sicher unglaublich kompliziert, aus einem Wort ein Rätsel zu machen, aus dem am Ende ein so einfaches Diagramm purzelt.
Meine Versuche, mit Dritteln zu rechnen, haben immer bei einigen Buchstaben neue Brüche ergeben.
Ich versuch' es demnächst nochmal.